Filtri matriciali

I vari filtri (quali la riduzione gaussiana, la tracciatura dei contorni, la sfocatura ...) sono realizzati tramite un' operazione di convoluzione, ovvero tramite una sorta di moltiplicazione strana tra 2 entità, l' immagine ed una matrice che fa da filtro (mi scuso con gli ingegneri per questa definizione insensata di convoluzione, ma esula dalla trattazione, è solo per chiarire un pelino la formula che andrò a spiegare).
Chiariamo meglio questo discorso; l' operazione di filtro (qualsiasi effetto) è fatta su di un pixel particolare (come per gli effetti precedenti) ma prendendo in considerazione anche i pixel adiacenti (per semplificare prendiamo solo gli 8 pixel attorno, poi il metodo è lo stesso anche per matrici più grandi).
Come si fa a prendere in considerazione il pixel centrale e gli altri 8 pixel attorno? usando una matrice di 9 elementi (in cui l' elemento centrale è il pixel interessato e gli altri 8 esterni sono appunti i pixel adiacenti), in cui i vari elementi sono dei valori che indicano il "peso" che ciascun pixel ha.

Ora vado a chiarire questa matrice, poi passerò alla formula.

La matrice di filtro è composta ad esempio così (il pixel centrale è il pixel da filtrare e pure lui ha un "peso"):

oppure oppure ...

Oltre agli elementi della matrice, bisogna specificare anche altri 2 parametri della matrice di filtro:
- Fattore (default 1) indica una costante di proporzione (va a dividere la sommatoria presentata più avanti)
- Offset (default 0) indica una costante da sommare algebricamente al risultato dell' intera formula

Calcolo del pixel:

PER OGNI pixel {
   PER OGNI canaleRGB {
      SOMMATORIA(n: 1->9) { canaleRGB(del pixel n) * peso(dell' elemento n della matrice) }
      coloreFiltrato = SOMMATORIA / Fattore + Offset
      SE coloreFiltrato < 0 ALLORA coloreFiltrato = 0
      SE coloreFiltrato > 0 ALLORA coloreFiltrato = 255
      canaleRGB = coloreFiltrato
   }
}

Come si vede dall' algoritmo, il "coloreFiltrato" è dato da questa formula:



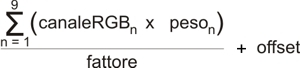
dove "n" sta per il numero del pixel preso in considerazione e del rispettivo valore nella matrice.
Alla fine si tratta semplicemente di fare il prodotto tra la componente del colore del pixel n con il valore dell' elemento n della matrice ... infine si sommano tutti e 9 i prodotti, si divide il tutto per il fattore e si somma l' offset ...
Questo per tutte e 3 le componenti RGB ...
Infine il solito controllo che i valori siano compresi tra 0 e 255.

Volendo personalizzare questi filtri matriciali, è possibile estendere l' elaborazione anche ad altri pixel adiacenti il pixel interessato ... ad esempio usando matrici 5x5 (ovvero considerando 25 pixel, cioè 24 pixel attorno), etc etc ...

Da notare comunque che i pixel nei bordi dell' immagine non vanno elaborati in quanto la matrice uscirebbe dai bordi dell' immagine:



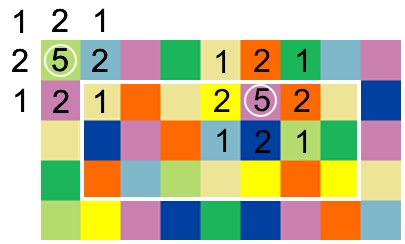
Come si può vedere, la matrice in angolo non può essere elaborata perchè va ad interessare zone in cui non ci sono pixel dell' immagine (si potrebbe assegnare dei colori arbitrari nel caso la matrice uscisse dall' immagine, ma non si otterrebbe un buon risultato). La matrice al centro invece prende in esame anche i bordi e sta dentro all' immagine.
Dunque sono da elaborare solamente i pixel all' interno del riquadro.